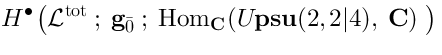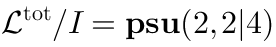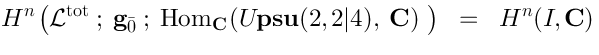Relation to the cohomology of the ideal

We now look at the relative Lie algebra cohomology:

(46)

There is an ideal such that:

(47)

This ideal consists of those combinations of the covariant derivatives which vanish in the vacuum . It turns out that the relative cohomology (46) coincides with the cohomology of :

(48)

The proof is in the paper.

We will therefore proceed to study .