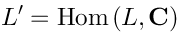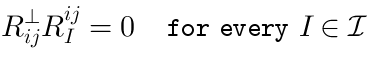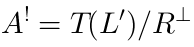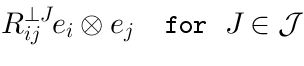Dual algebraWe have just defined a quadratic algebra.
Now we will define the dual algebra, which is denoted
.
Consider the linear spacewhich is dual to
:
As we introduced the basisin
, we can introduce the dual basis
in
. “Dual basis” means:
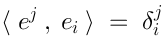
Remember thatwas defined using the set of constant matrices
, which were used to define the quadratic constraints (3). Consider the linear space of all the matrices
orthogonal to every
. “Orthogonal” means that
satisfies the equation:
Suppose that,
is a set of linearly independent solutions of this equation. Let us consider:
whereis generated by the tensors of the form:
Conclusion: We started from a quadratic algebra
and constructed another quadratic algebra
, which is called quadratic dual to
.