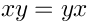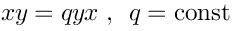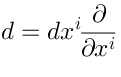IntroductionTheoretical physics has traditionally been very close to geometry.But more recently it appears that our mathematical guide should be algebra, not geometry. It seems that geometrical constructions (such as smooth manifold in its traditional definition) are an artifact of taking the classical limit. Quantum mechanics, on the other hand, is based on algebra.
It would seem that some theoretical physics constructions could become more useful if translated into algebraic language.
Algebraically speaking, what is smooth manifold? Smooth manifold can be identified as a commutative algebra, namely the algebra of functions on this manifold. For exampleis identified with the algebra formed by two letters
and
with the relation:
Now, we can deform this algebra. For example:This is the noncommutative. We can ask ourselves how various geometrical constructions generalize to the noncommutative case.
In my talk I will discuss the technique which evolved around the noncommutative generalization of the de Rham differential. The commutative de Rham differencial is:
But what happens if we consider noncommutative? How to generalize
, and what would be its properties?
It turns out that this question is quite relevant to modern string worldsheet theory (Berkovits formalism).