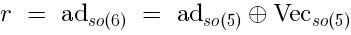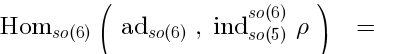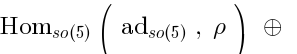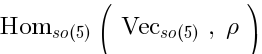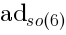Let us return to our case. We want to demonstrate that there are no excitations transforming in the adjoint of. So, we consider the special case of Frobenius reciprocity when
is the adjoint rep of
We have to go over all the tensor representationsand verify if
enters into
using Eq. (5). We observe:
(the decomposition of) Now Eq. (5) reads:
[antisymm. tensors]
[vectors]
The Type IIB SUGRA does not contain vectors, although does contain antisymmetric tensors:
and
.
But in the space of 2-forms on
, the only subspace transforming in the adjoint of
where
. But these are unphysical, a total gauge:
.
This concludes the proof, that these are no states transforming in
The same conclusion can be reached by looking at the tables in the paper of H. J. Kim, L. J. Romans and P. van Nieuwenhuizen
