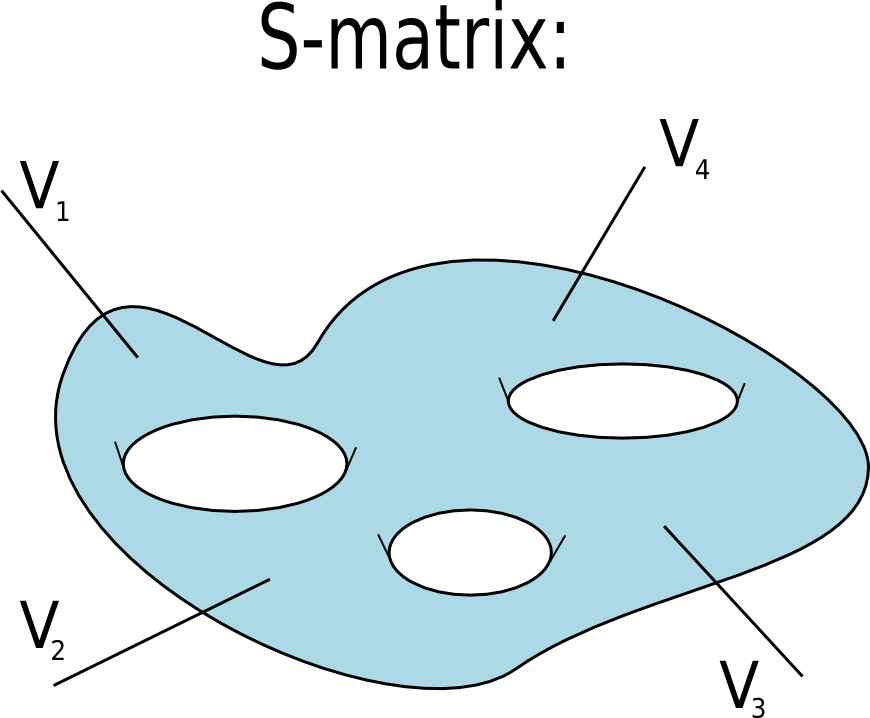
Introduction
I will talk about some aspect of the superstring perturbation theory.
In order to compute the S-matrix, we sum over the Riemann surfaces with the insertions of
vertex operators:
It is essential, that there are two types of vertex operators: integrated and unintegrated.
When we talk about the Hilbert space of the theory (= BRST cohomology), it is usually described in terms of the
unintegrated vertices. Integrated vertices, on the other hand, describe the deformations of the
string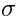 
-model.
-model.In the calculation of the scattering amplitudes, we need to know both types of operators.
They form the same space of states, there is a one-to-one correspondence between them: the descent procedure. We will give some algebraic interpretation of this descent procedure, which hopefully makes it more transparent.
We will start with a very brief review of the pure spinor superstring.