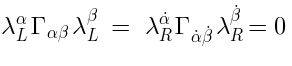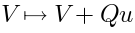Unintegrated vertices
Definition 1: “Operators” are reasonably nice expressions built on
the sigma-model fields and their derivatives, modulo the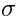 
-model classical equations of motion.
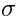-model classical equations of motion.The sigma-model fields are typically matter fields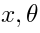 
and ghosts 
.
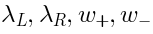The ghosts 
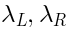satisfy the pure spinor constraints:
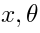and ghosts .
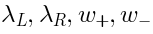The ghosts 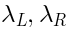satisfy the pure spinor constraints:
Definition 2:
The conformal dimension of an operator is defined as the total number of derivatives, plus the number of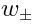 
.
The BRST operator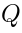 
, being a symmetry of the theory, acts on such expressions.
Definition 3:
The ghost number of an operator is the total number of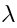 
’s minus the total number of 
.
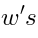Definition 4:
Unintegrated vertex is an operator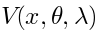 
of the conformal dimension zero
and ghost number two, annihilated by .
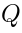The gauge transformation of the vertex operator is:
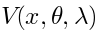of the conformal dimension zero
and ghost number two, annihilated by .
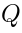The gauge transformation of the vertex operator is:
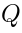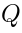Unintegrated operators form the cohomology of the BRST operator at the ghost number two.
This is, essentially, the Hilbert space of states in the worldsheet sigma-model
at the ghost number two.
This is, essentially, the Hilbert space of states in the worldsheet sigma-modelIt is a fundamental principle of the string theory, that every state corresponds to some deformation of the worldsheet theory. This leads to the concept of integrated vertex, which we will now describe.