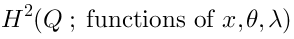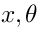Unintegrated vertices

Unintegrated vertices correspond to the cohomology of at the ghost number 2:

(16)

The tangent space to the space of SUGRA backgrounds is (16). Notice that depends on the background — different points have different tangent spaces!

Sometimes it is more convenient to work with the dual space to (16). Dilaton, Riemann-Christoffel symbol, -field, ... , are all measurable quantities on the deformations. For a small deformation of the background, we can ask “what is the corresponding variation of the dilaton? of the curvature?” etc. These are all local gauge-invariant observables.

The space of local gauge-invariant observables can be understood as follows:

• the dual space to the cohomology (16) of on the polynomial functions of

A convenient description of this dual space, at least in flat space and in , can be obtained using the mathematical formalism of Koszul duality.