Closer look at
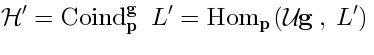 This is, essentially, the space of linear functions on
This is, essentially, the space of linear functions on, with values in
, invariant under the action of
.
Let us introduce the coordinates onin the following way.
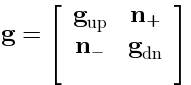 In other words, every element of
In other words, every element ofcan be decomposed as a sum
where
,
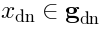
and
. Therefore elements of
can be thought of as linear functions from monomials to elements of
:
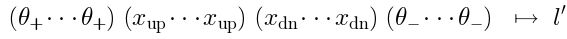 Invariance under
Invariance underimplies that
is only nonzero when there are no
, and moreover the value of
on monomials involving
and
can be calculated from the value on the monomials only involving
.
We conclude that
can be realized as the space of functions of
, taking values in
.