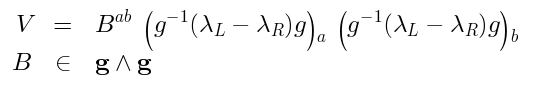Counter-example at low momentumThe theorem does not work for those representations which have low spins in.
For example, consider the beta-deformation. The corresponding vertex was studied in my paper “Notes on beta-deformations of the pure spinor superstring in
” with O.A. Bedoya, L.I. Beviláqua and V.O. Rivelles, arXiv:1005.0049.
It is parametrized by a constant antisymmetric tensor:
But there is a gauge symmetry parametrized by a constant:
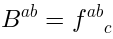 (If
(Ifis of such form, then the deformation (5) can be undone by the field redefinition.)
This means that actually the space of deformations of the form (5) is not
but rather
.
But to write the Eq. (5) for the vertex we need to pick a representative
. Actually, in this case the covariant vertex does not exist. This is because of the low spin; the existence theorem (2) only works for “high enough spin”.