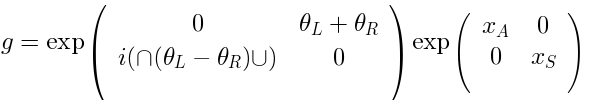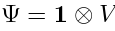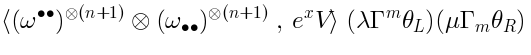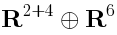Explicit formula for dilaton profileWe use the following parametrization of:
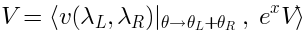 After adding some BRST-exact terms the leading term of the
After adding some BRST-exact terms the leading term of the-expansion is proportional to:
We obtainand
where:
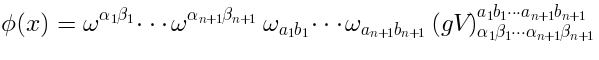 In this formula
In this formulaparametrizes the bosonic space
.
The expression foris more transparent in the vector notations. Let us think of
as the symmetric traceless tensor of
(the upper latin indices) and the symmetric traceless tensor of
(the lower greek indices). We parametrize the point of
as a pair of vectors
,
. We get:
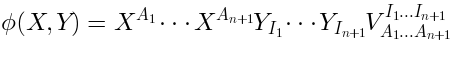 We conclude that the dilaton profile is polynomial in the coordinates of “two-time physics”
We conclude that the dilaton profile is polynomial in the coordinates of “two-time physics”