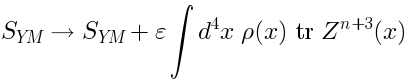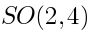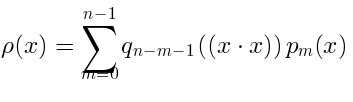Finite-dimensional example: view from SYM

By AdS/CFT the non-normalizable excitations correspond to the deformations of the SYM action:

    (16)

where is a complex combination of the SYM scalars and is a density of the conformal weight . We observe that:

1. for any integer the space of densities has a finite-dimensional subspace invariant under the conformal group

2. Acting on this space by the supersymmetries we generate a finite-dimensional representation of the full superconformal group

Point 2 is obvious given 1. To explain 1, we observe that the deformation (16) is conformal-invariant if we transform as a “density” of weight :

    

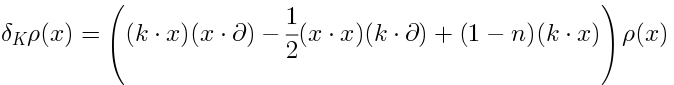Consider the linear space consisting of the densities of the following form:

    (17)

where is a homogeneous polynomial in of degree , and a polynomial in of degree (not necessarily homogeneous). One can see this space is closed under the action of the conformal transformations. This means that the (infinite-dimensional) representation of the conformal group in the space of densities of the weight for has an invariant finite-dimensional subspace consisting of the densities of the form (17).

There is no invariant complementary subspace, therefore the space of densities is not a semisimple representation of .