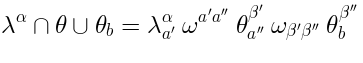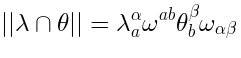The structure of: preliminaries
It remains to explain what is.
We have to remember the
-covariance condition (4) on
. It implies that the construction of
should be covariant under the local Lorentz transformations
. It is convenient to consider complexified symmetry algebras:
and
. The spinors transform in the fundamental representation of
and antifundamental of
:
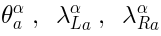 The
Theis characterized as the subalgebra preserving the symplectic forms
and
, which are both given by the
-matrices
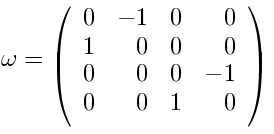 This allows to write covariant chains of letters
This allows to write covariant chains of lettersand
linked with
, for example: