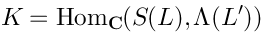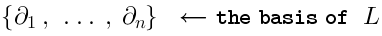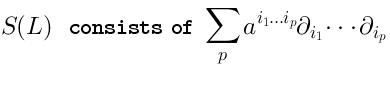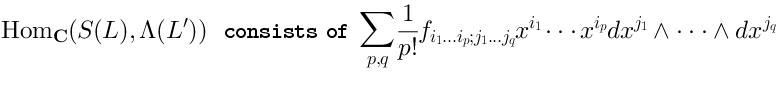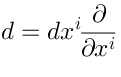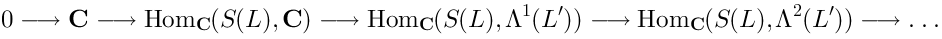De Rham complexAs a partucular example, let us consider,
. In this case we get:
This is the de Rham complex for the flat space.
Explanation:
Ouris an
-dimensional vector space. Let us introduce a basis and call the basis elements
:
(this is just a notation, just use letterinstead of
). What is
? It is the space of polynomials of
, i.e.:
And what is the dual space? It is the space of “Taylor series”:
The dual spacehas the following basis:
Finally, what is? Here it is:
The De Rham differential acts as usual:
This operator is nilpotent. Moreover, it provides the resolution ofin the sense that the following complex:
is exact.Mathematically speaking, the de Rham complex provides:
An injective resolution of the
module