Consider the following space:
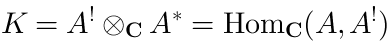
| (10) |
- the space of linear maps from
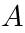
to
.
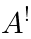
It turns out that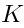 
naturally comes with some nilpotent operator 
,
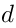which is a noncommutative generalization of the de Rham complex.
We will explain this using the particular example (8), (9)
of dual algebras; in that particular case 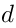is exactly the de Rham differential.