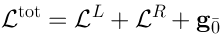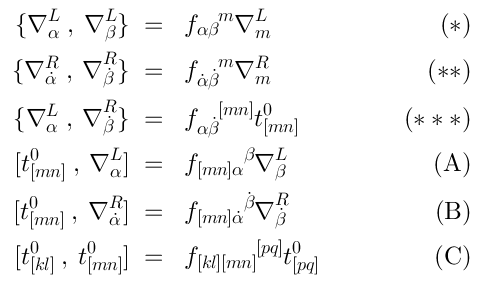Definition of the Lie algebra

We will start with . We define the Lie algebra as a sum of two copies of , plus some finite-dimensional Lie algebra (as linear spaces):

                 (38)

which are all “glued together” as follows:

(39)

where is the structure constants of — the algebra of supersymmetries of .   Comments:

1. Our is not a quadratic algebra (because of Eqs. (A), (B) and (C))

2. Eq. (*) defines a quadratic subalgebra which we call , and Eq. (**) defines

3. Each and is the same as the Yang-Mills (or Maxwell) algebra (20)

4. The rest of relations tell us how to “glue together” and

5. Eq. (C) tells us that the generators form — rotations around a point in