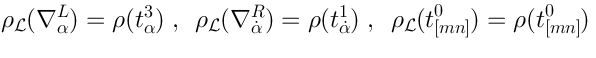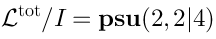Relative cohomology

Consider any representation of . It is also a representation of :

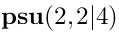
is a representation of is a representation of      

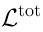
Indeed, let us remember the structure of the . The generators are:
The subalgebra is generated by . To have a representation of means to have operators , , , acting in the linear space .
We then define the action of in in terms of the action of :

     

This is consistent. In fact, there is an ideal such that
We defined so that .