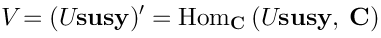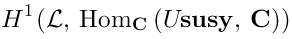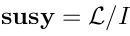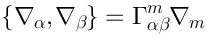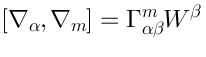Example: Maxwell theory

For example, consider the supersymmetric Maxwell theory in 10D in flat space. In the coset space approach, the flat space can be described as a group manifold of the Lie group , which is generated by supersymmetries plus Poincare translations.

Solutions of the equations of motion correspond to the ghost number 1 vertex operators. The BRST complex is based on the functions of and :
                
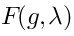
The space of functions (or, rather, the Taylor series) is dual to the universal enveloping algebra .

This is true for any group with the Lie algebra . The universal enveloping algebra can be identified with the left-invariant differential operators on of finite order, i.e. expressions of the form:
                
where . Then given a function on , we can compute the derivative of at the unit :
                
This requires the knowledge of the coefficients of the Taylor series of at .
Therefore we observe the duality relation between the functions on and the elements of the universal enveloping algebra .

Therefore in this case:

(26)

Then Koszul duality (25) tells us that the space of vertex operators is:

(27)

The relation between and is the following:

(28)

where is some ideal.

This is just to say that the algebra “is a solution” to the Yang-Mills constraint:
           (*)
in the following sense. If we put — the generator of the supersymmetry transformation, then the constraint is satisfied. The definition (20), (22) of is such that is the most general (“universal”) Lie algebra satisfying this constraint; therefore any algebra satisfying the Yang-Mills constraint should be a factoralgebra of by some ideal.

The ideal can be described rather explicitly, in the following manner. Because of the quadratic relation (*), is proportional to :

(29)

(this is the definition of ). It turns out, as a consequence of (*), that:

(30)

So defined generates the ideal             

Simply put, this ideal consists of the elements of the algebra which vanish in the vacuum.