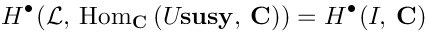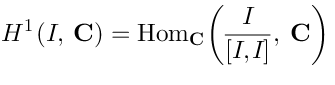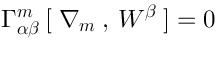Using the Shapiro’s lemmaOne can show that:In particular, the vertex operators (corresponding to) are:
This formula may seem mysterious, but it has a transparent physical meaning. Indeed, it implies that the space of solutions of super-Maxwell equations is dual (as a linear space) to the space generated byand its derivatives
.
This is what we expect:
and its derivatives exhaust the gauge-invariant operators, i.e. gauge invariant linear functionals on the space of Maxwell solutions. Therefore:
This approach leads to the classification of gauge-invariant operators
Notice thatautomatically satisfies the Dirac equation: