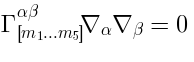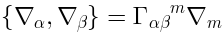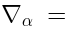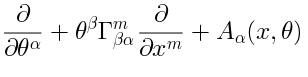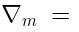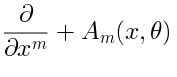Algebra formed by covariant derivatives
We will start by relating the cohomology of (6) with some Lie algebra cohomology.
Pure spinor cohomology is related to the Lie algebra cohomology of some infinite-dimensional Lie superalgebra
So, we have to first define that infinite-dimensional Lie superalgebra. The definition is motivated by the super-Yang-Mills theory, and the resulting algebra is called SYM.
Let us proceed to its definition.
Classical equations of motion of the ten-dimensional super-Yang-Mills algebra are encoded in the constraints:
As a consequence of these constraints, there exist operators 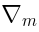 such that:
such that:
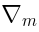 such that:
such that:
The actual definition of the operators 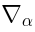 and
and 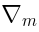 in the super-Yang-Mill theory is:
in the super-Yang-Mill theory is:
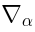 and
and 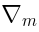 in the super-Yang-Mill theory is:
in the super-Yang-Mill theory is:
I am sorry for the abuse of notations; notice that 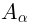 and
and 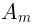 are completely different fields;
but in my notations the only difference between them is greek subindex
are completely different fields;
but in my notations the only difference between them is greek subindex 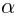 vs. latin subindex
vs. latin subindex 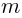 .
.
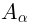 and
and 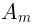 are completely different fields;
but in my notations the only difference between them is greek subindex
are completely different fields;
but in my notations the only difference between them is greek subindex 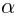 vs. latin subindex
vs. latin subindex 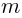 .
.Now let us forget about the ``internal structure'' of 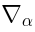 and
and 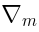 given by (9)
and (10) and think of Eq. (7) as defining
relations in an
abstract algebra formed by the letters
given by (9)
and (10) and think of Eq. (7) as defining
relations in an
abstract algebra formed by the letters  .
.
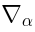 and
and 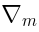 given by (9)
and (10) and think of Eq. (7) as defining
relations in an
abstract algebra formed by the letters
given by (9)
and (10) and think of Eq. (7) as defining
relations in an
abstract algebra formed by the letters  .
. This is an infinite-dimensional algebra. Moreover, this is actually a quadratic algebra, because the constraint (7) is quadratic in generators.