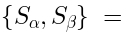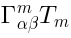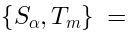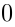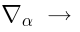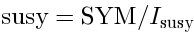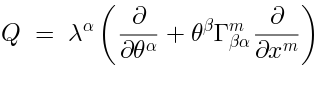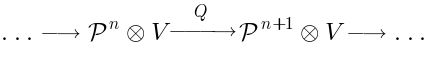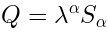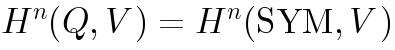BRST cohomology vs Lie algebra cohomology
1 Relation between the SYM algebra and the susy algebra
The Lie superalgebra 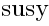 is formed by the operators
is formed by the operators 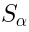 and
and 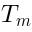 with the following commutation relations:
with the following commutation relations:
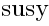 is formed by the operators
is formed by the operators 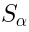 and
and 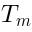 with the following commutation relations:
with the following commutation relations:
The algebra 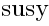 (unlike SYM algebra) is finite-dimensional.
There is a homomorphism from the SYM algebra to
(unlike SYM algebra) is finite-dimensional.
There is a homomorphism from the SYM algebra to 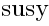 :
:
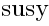 (unlike SYM algebra) is finite-dimensional.
There is a homomorphism from the SYM algebra to
(unlike SYM algebra) is finite-dimensional.
There is a homomorphism from the SYM algebra to 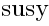 :
:
The kernel of this homomorphism is an ideal in SYM, which we will call 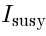 . We have:
. We have:
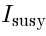 . We have:
. We have:
2 Cohomology of SYM algebra and pure spinor cohomology
Now we want to relate the cohomology of the operator (6) to the cohomology of the Lie superalgebra SYM.
We observe that the components of pure spinor 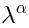 get contracted with the differential operators
get contracted with the differential operators
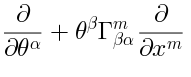 which form a representation of the algebra
which form a representation of the algebra 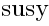 (11).
(11).
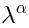 get contracted with the differential operators
get contracted with the differential operators
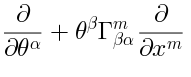 which form a representation of the algebra
which form a representation of the algebra  (11).
(11).Let us therefore consider any representation 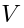 of
of 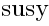 .
To every such representation corresponds a pure spinor BRST complex, which is constructed as follows.
.
To every such representation corresponds a pure spinor BRST complex, which is constructed as follows.
Let 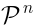 be the space of polynomials of the pure spinor variables
be the space of polynomials of the pure spinor variables 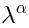 of degree
of degree 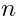 . It is assumed that
. It is assumed that 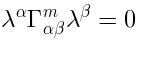 ; in other words
; in other words
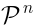 is the commutative algebra of polynomials of the degree
is the commutative algebra of polynomials of the degree 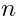 of the variables
of the variables 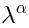 modulo the
ideal of polynomials divisible by the expression
modulo the
ideal of polynomials divisible by the expression 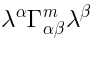 .
.
where the BRST operator acts as follows (compare to (14)):
The action of 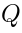 on
on 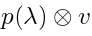 where
where 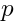 is a polynomial of degree
is a polynomial of degree 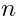 of
of 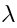 and
and 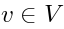 is equal to
is equal to 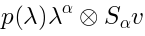 . Notice that
. Notice that 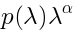 is a polynomial
of the degree
is a polynomial
of the degree 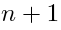 in
in 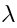 , so we got an element of
, so we got an element of 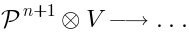 .
.
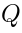 on
on 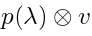 where
where 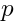 is a polynomial of degree
is a polynomial of degree 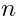 of
of 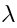 and
and 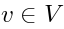 is equal to
is equal to 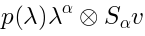 . Notice that
. Notice that 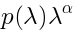 is a polynomial
of the degree
is a polynomial
of the degree 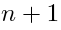 in
in 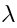 , so we got an element of
, so we got an element of 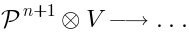 .
.The cohomology of this complex is related to the Lie algebra cohomology of the SYM algebra.
In order to explain how, we have to notice that 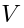 , being a representation of
, being a representation of 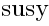 , is also a representation of
, is also a representation of 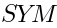 (because of the homomorphism (12)). Then we have:
(because of the homomorphism (12)). Then we have:
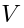 , being a representation of
, being a representation of 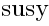 , is also a representation of
, is also a representation of 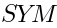 (because of the homomorphism (12)). Then we have:
(because of the homomorphism (12)). Then we have:
|
This is a very nontrivial theorem. Our goal is to establish a similar theorem in the SUGRA context.
An important special case is when 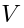 is
the dual space of the universal enveloping algebra of the
is
the dual space of the universal enveloping algebra of the 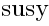 algebra:
algebra:
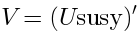 This is the representation in the space of Taylor series of functions on the super-space-time.
In this case the cohomology of the BRST complex computes the solutions of the Maxwell equations.
In this case the operator (17) becomes precisely (14).
This is the representation in the space of Taylor series of functions on the super-space-time.
In this case the cohomology of the BRST complex computes the solutions of the Maxwell equations.
In this case the operator (17) becomes precisely (14).
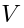 is
the dual space of the universal enveloping algebra of the
is
the dual space of the universal enveloping algebra of the 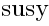 algebra:
algebra:
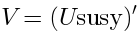 This is the representation in the space of Taylor series of functions on the super-space-time.
In this case the cohomology of the BRST complex computes the solutions of the Maxwell equations.
In this case the operator (17) becomes precisely (14).
This is the representation in the space of Taylor series of functions on the super-space-time.
In this case the cohomology of the BRST complex computes the solutions of the Maxwell equations.
In this case the operator (17) becomes precisely (14).