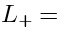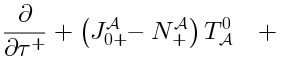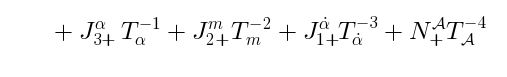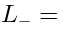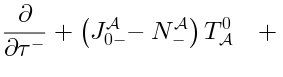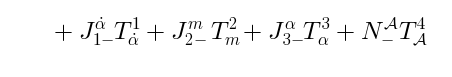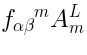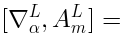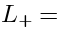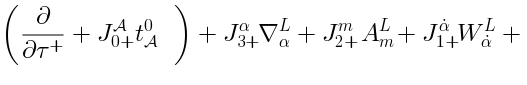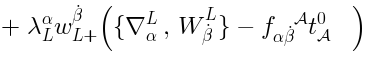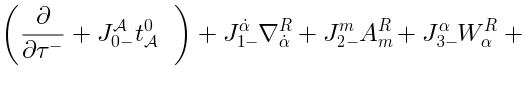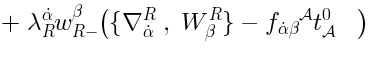Generalizations of the Lax pair
1 Lax operator and the loop algebra
One can interpret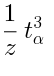 
, 
, 
,
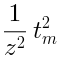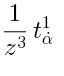as generators of the
twisted loop superalgebra 
.
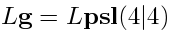The word ``twisted'' means that the power of the spectral parameter mod 4 should
correlate with the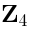 
-grading of the generators
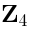-grading of the generators
where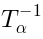 
replaces 
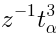etc.; operators 
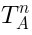are generators of the
twisted loop superalgebra. Withe these new notations, the spectral parameter
is not present in 
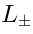. Instead of entering explicitly in 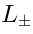, it now
parametrizes a representation of the generators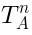 
.
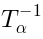replaces 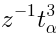etc.; operators 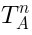are generators of the
twisted loop superalgebra. Withe these new notations, the spectral parameter
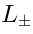is not present in . Instead of entering explicitly in 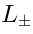, it now
parametrizes a representation of the generators 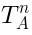.2 Further generalization
The basic relations (23) imply:
and similar equations for the commutators of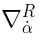 
.
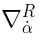.Eq. (36) we already discussed; it encodes the SUGRA constraints and at the same time defines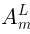 
.
Eq. (37) is a theorem-definition: the theorem says that the left hand side is proportional
to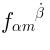 
, and the definition is of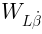 
.
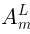Eq. (37) is a theorem-definition: the theorem says that the left hand side is proportional
to 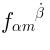, and the definition is of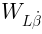 It turns out, that there is the following generalization of the Lax pair:
