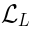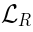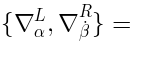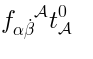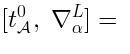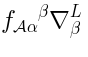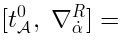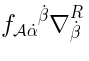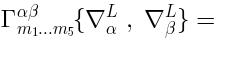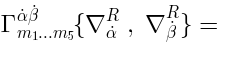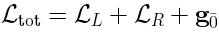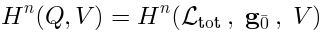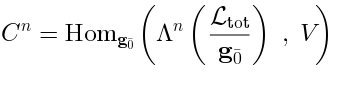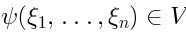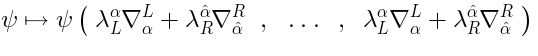Algebra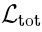 
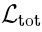
We will now extend the superconformal algebra to some infinite-dimensional algebra, just like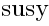 
was extended to SYM.
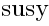was extended to SYM.1 Definition
In other words:
The consistency of this definition can be verified using the general theory of quadratic-linear
algebras, the PBW theorem by Polishchuk-Positselski-Braverman-Gaitsgory.
Since the associated graded algebra is Koszul, it is enough to verify
the Jacobi identity for three elementary generators. But for any three elementary generators, the commutation
relations are the same as in the twisted loop algebra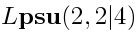 
.
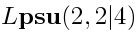.2 BRST cohomology as a relative cohomology
The analogue of (17) is:
It involves relative Lie algebra cohomology. The cochain complex consists of
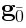-invariant linear functions:
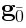-invariant linear functions:
|
Therefore an element of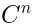 
is a function of 
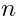Lie-algebra valued variables with taking values in 
:
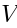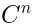is a function of 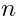Lie-algebra valued variables with taking values in :
|
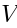The actual map between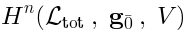 
and 
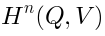goes as follows. Given a representative cocycle 
,
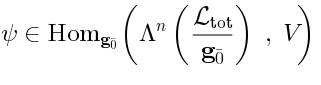the representative of the corresponding element in 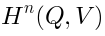is obtained by the substitution of
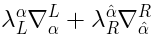in place of
:
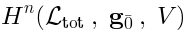and
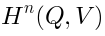goes as follows. Given a representative cocycle ,
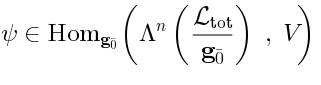the representative of the corresponding element in 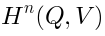is obtained by the substitution of
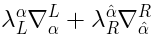in place of
:
