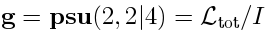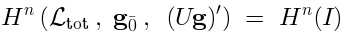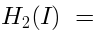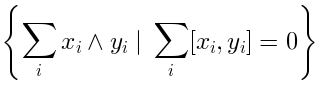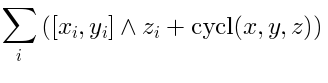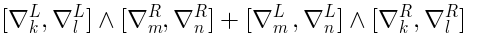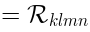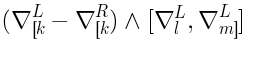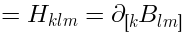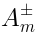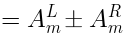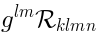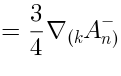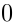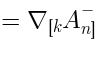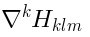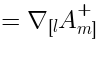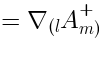My Ideal
Algebraic interpretation of SUGRA operators
There is a relation analogous to (
13), namely exists an ideal
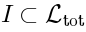
such that:
This has an interesting consequence in the case when
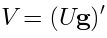
:
In particular, the linear space dual to
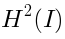
:
| | | | |
| | modulo 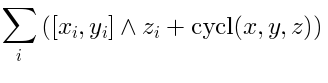 |
| | |
describes
gauge invariant local operators. The analysis of (
28) is nontrivial, the only
operator in AdS which I can identify is the
dilaton
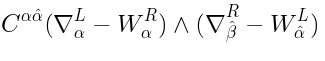
where
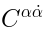
is some
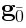
-invariant tensor and
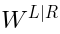
is defined in (
37).
In the
flat space limit, the analysis simplifies:
We get the following equations of motion:
The gradient of the dilaton corresponds to
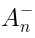
, while
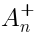 does not have a
clear interpretation
does not have a
clear interpretation in the Type IIB supergravity.
This rizes a question: do we correctly understand the low momentum sector of the Type IIB SUGRA?
The pure spinor formalism suggests a different low momentum spectrum from what we all know from the textbooks.
Is it possible that the textbooks miss some discrete degrees of freedom?
But we will now turn to a different subject. Let us look at what we can learn from the
classical integrability of the worldsheet theory.
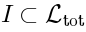 such that:
such that:
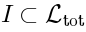 such that:
such that:
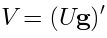 :
:
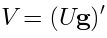 :
:
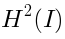 :
:
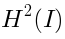 :
:
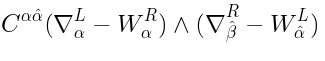 where
where 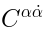 is some
is some 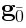 -invariant tensor and
-invariant tensor and 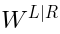 is defined in (37).
In the flat space limit, the analysis simplifies:
is defined in (37).
In the flat space limit, the analysis simplifies:
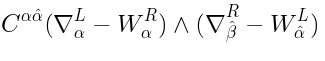 where
where 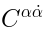 is some
is some 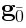 -invariant tensor and
-invariant tensor and 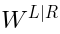 is defined in (37).
In the flat space limit, the analysis simplifies:
is defined in (37).
In the flat space limit, the analysis simplifies:
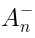 , while
, while 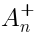 does not have a
clear interpretation in the Type IIB supergravity.
does not have a
clear interpretation in the Type IIB supergravity.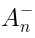 , while
, while 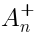 does not have a
clear interpretation in the Type IIB supergravity.
does not have a
clear interpretation in the Type IIB supergravity.