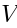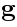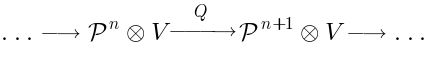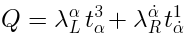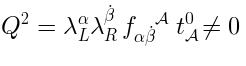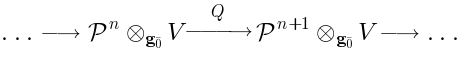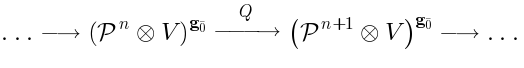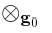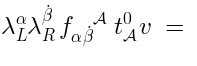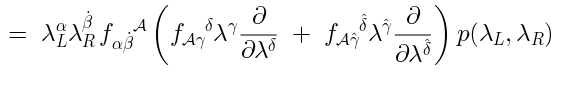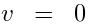BRST cohomology of Type IIB in 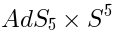
We want to construct some analogue of (
15), (
16) where the algebra
would be replaced with the superconformal algebra
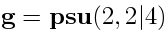
.
The simplest naive guess: given any representation
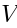
of
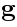
, consider the same complex as in
(
15):
where now
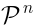
is the space of
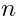
-th degree polynomials of
two pure spinors
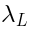
and
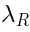
and the operator
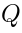
is defined just as a sum of two expressions like (
16):
This is almost correct, except for such an operator would not be nilpotent:
The way out is to impose some condition of
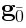
-invariance, either this:
or maybe this:
Imposing such an invariance condition makes
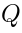
nilpotent. For example, in case of (
18):
This is zero because of the Jacobi identity and pure spinor constraints.
Eq. (19) is the correct definition of the BRST complex, and the one which actually comes from
the pure spinor formalism.
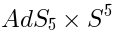
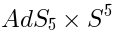
 would be replaced with the superconformal algebra
would be replaced with the superconformal algebra 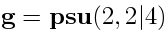 .
. would be replaced with the superconformal algebra
would be replaced with the superconformal algebra 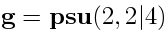 .
.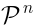 is the space of
is the space of 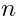 -th degree polynomials of two pure spinors
-th degree polynomials of two pure spinors 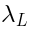 and
and 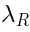 and the operator
and the operator 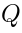 is defined just as a sum of two expressions like (16):
is defined just as a sum of two expressions like (16):
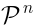 is the space of
is the space of 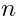 -th degree polynomials of two pure spinors
-th degree polynomials of two pure spinors 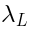 and
and 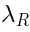 and the operator
and the operator 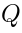 is defined just as a sum of two expressions like (16):
is defined just as a sum of two expressions like (16):
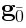 -invariance, either this:
-invariance, either this:
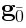 -invariance, either this:
-invariance, either this:
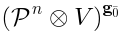 is the space of
is the space of 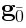 -invariants,
while
-invariants,
while 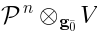 are ``co-invariants''. When
are ``co-invariants''. When 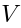 is finite-dimensional, they are the same.
But we often need infinite-dimensional
is finite-dimensional, they are the same.
But we often need infinite-dimensional 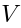 such as
such as 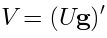 . In this case, we typically need (19).
. In this case, we typically need (19).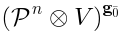 is the space of
is the space of 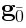 -invariants,
while
-invariants,
while 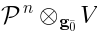 are ``co-invariants''. When
are ``co-invariants''. When 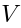 is finite-dimensional, they are the same.
But we often need infinite-dimensional
is finite-dimensional, they are the same.
But we often need infinite-dimensional 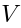 such as
such as 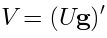 . In this case, we typically need (19).
. In this case, we typically need (19).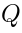 nilpotent. For example, in case of (18):
nilpotent. For example, in case of (18):
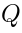 nilpotent. For example, in case of (18):
nilpotent. For example, in case of (18):