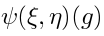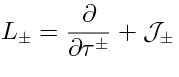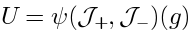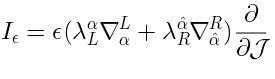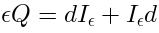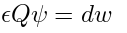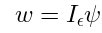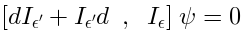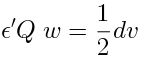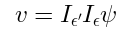Integrated Vertex in AdS
Finally, we are now ready to discuss our construction of the integrated vertex.
1 Construction of the integrated vertex
Suppose that we are given an unintegrated vertex, and we want to construct the corresponding integrated vertex.
Unintegrated vertices correspond to the elements of 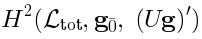 .
The 2-cocycle
representing such an element is a bilinear function of two elements of
.
The 2-cocycle
representing such an element is a bilinear function of two elements of 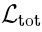 ,
which we will denote
,
which we will denote 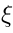 and
and 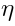 . We have to remember that the 2-cocycle takes
values in
. We have to remember that the 2-cocycle takes
values in 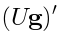 which is identified with the space of Taylor series at the
unit of the group manifold. Let
which is identified with the space of Taylor series at the
unit of the group manifold. Let 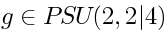 denote the group element.
denote the group element.
Therefore, the element
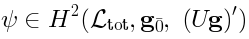
is a function
of two elements of
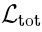
, which we will call
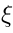
and
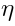
, taking values in the functions of
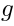
:
Remember that our generalized Lax operators (
38), (
39) have the form:
where
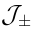
are operators of the conformal dimension 1 taking values in
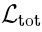
.
Theorem 8: The integrated vertex operator is obtained from (42)
by replacing 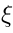 and
and 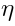 with
with 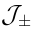 :
:
2 Proof of the descent procedure
We have to verify the descent procedure (5), (4).
The proof is a variation of the famous differential geometry formula 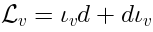 .
.
Consider 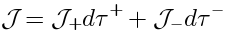 . This is a
. This is a 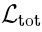 -valued differential
1-form on the worldsheet. Substitution of
-valued differential
1-form on the worldsheet. Substitution of 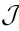 into
into 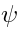 intertwines the
intertwines the 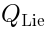 with the de Rham
differential
with the de Rham
differential 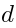 . (The verification of this statement uses the fact that
. (The verification of this statement uses the fact that 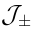 satisfies
the zero-curvature equations (40).)
satisfies
the zero-curvature equations (40).)
It is useful to introduce the free Grassmann parameters
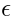
and
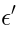
. Let us formally introduce the operator
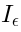
as follows:
This operator simply replaces
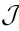
with
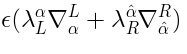
—
cp. Eq. (
27).
Eq. (
41) implies that the BRST differential acts as follows:
But
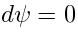
, therefore:
This was the first step (
5) of the descent procedure.
To make the second step (
4),
we have to remember that
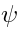
is a
relative cocycle, which means that it always vanishes whenever
one of the ghosts falls into
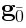
. This implies:
and further:
Notice that the unintegrated vertex
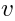
is obtained from the cocycle
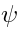
by replacing the ghost
fields with
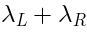
,
as it should be.
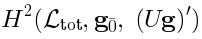 .
The 2-cocycle
representing such an element is a bilinear function of two elements of
.
The 2-cocycle
representing such an element is a bilinear function of two elements of 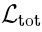 ,
which we will denote
,
which we will denote 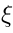 and
and 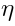 . We have to remember that the 2-cocycle takes
values in
. We have to remember that the 2-cocycle takes
values in 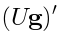 which is identified with the space of Taylor series at the
unit of the group manifold. Let
which is identified with the space of Taylor series at the
unit of the group manifold. Let 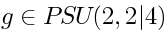 denote the group element.
denote the group element.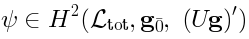 is a function
of two elements of
is a function
of two elements of 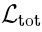 , which we will call
, which we will call 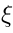 and
and 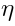 , taking values in the functions of
, taking values in the functions of 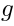 :
:
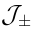 are operators of the conformal dimension 1 taking values in
are operators of the conformal dimension 1 taking values in 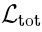 .
.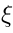 and
and 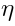 with
with 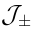 :
: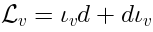 .
.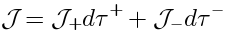 . This is a
. This is a 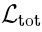 -valued differential
1-form on the worldsheet. Substitution of
-valued differential
1-form on the worldsheet. Substitution of 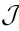 into
into 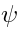 intertwines the
intertwines the 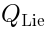 with the de Rham
differential
with the de Rham
differential 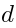 . (The verification of this statement uses the fact that
. (The verification of this statement uses the fact that 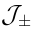 satisfies
the zero-curvature equations (40).)
satisfies
the zero-curvature equations (40).)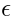 and
and 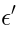 . Let us formally introduce the operator
. Let us formally introduce the operator
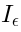 as follows:
as follows:
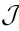 with
with 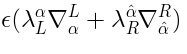 —
—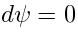 , therefore:
, therefore:
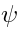 is a relative cocycle, which means that it always vanishes whenever
one of the ghosts falls into
is a relative cocycle, which means that it always vanishes whenever
one of the ghosts falls into 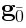 . This implies:
. This implies:
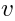 is obtained from the cocycle
is obtained from the cocycle 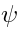 by replacing the ghost
fields with
by replacing the ghost
fields with 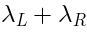 , as it should be.
, as it should be.